La finestra di dialogo utilizzata per il calcolo del flusso concatenato è mostrata nella Figura 7-9. La soluzione del potenziale scalare permette di determinare la fem indotta in condizioni di funzionamento a vuoto. Dato che la macchina a flusso assiale presenta una reattanza sincrona trascurabile, la fem calcolata è comunque molto simile a quella calcolata in condizioni di funzionamento sotto carico.
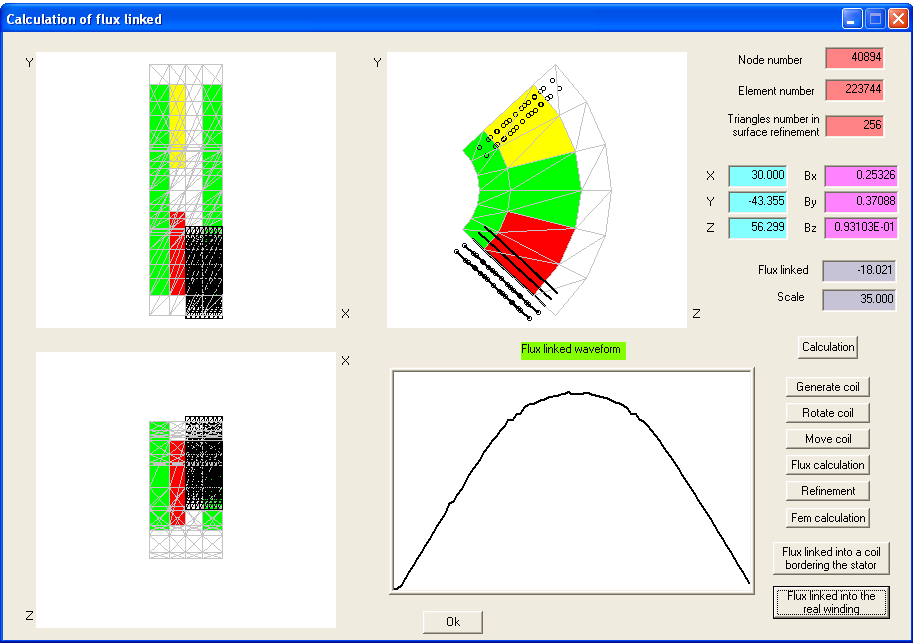
L’idea è quella di calcolare il flusso concatenato al variare della posizione angolare statore-rotore; interpolare i punti calcolati per ogni angolo elettrico per ottenere una funzione continua ed alla fine, calcolare la derivata per ottenere la fem indotta.
dove per si intende la velocità angolare della macchina.
Per calcolare la fem indotta negli avvolgimenti di macchina dalla soluzione del MSP, è possibile tener conto dell’accoppiamento magnetico tra i magneti permanenti montati sul disco rotorico e gli avvolgimenti di macchina.
Con questo tipo di accoppiamento, è necessario calcolare un coefficiente di accoppiamento del flusso concatenato, tra una fase di armatura ed il magnete permanente usando il calcolo dell’energia e una tecnica perturbativa.
Semplificando l’approccio è possibile affermare che il flusso concatenato con una bobina ideale vale l’integrale di superficie del prodotto scalare tra l’induzione magnetica e la superficie dS di orientazione :
Se si posiziona una bobina di sezione infinitesimale il flusso del vettore induzione può essere calcolato tramite la (7-18).
Dato che B viene ricavato in forma numerica, non è possibile risolvere la (7-18) in forma analitica. La discretizzazione 3D porta a suddividere la superficie della bobina ideale attraverso una mesh triangolare in 2D.
Il flusso concatenato nella bobina sarà approssimato dalla sommatoria dei prodotti scalari tra il campo di induzione magnetica B e la superficie triangolare. Il valore di B viene ricavato sul baricentro di ogni triangolo. Osservando l’esempio della Figura 7-10 la formulazione numerica per il flusso concatenato può essere scritta come:
La precisione del calcolo numerico del flusso concatenato aumenta con il numero di suddivisioni della triangolazione 2D. La suddivisione della superficie non deve comunque essere superiore al refinement della mesh 3D visto che all’interno di un elemento finito tetraedrico i valori del campo sono ottenuti solo per interpolazione.
Figura Calcolo analitico e numerico del flusso concatenato con una spira circolare infinitesima
Il flusso concatenato con la bobina ideale in funzione dell’angolo elettrico di macchina può essere determinato attraverso la rotazione della superficie S con qualsivoglia angolazione. Vista la geometria studiata la rotazione della bobina viene analizzata da 0° a 180° elettrici.
Il flusso di induzione magnetica in realtà, si concatena con una bobina massiccia che costituisce l’avvolgimento di fase avvolto intorno allo statore. La bobina massiccia presente dimensioni finite sia in direzione radiale che assiale. La bobina reale può essere simulata attraverso una serie di calcoli effettuati su bobine infinitesimali posti in vari punti dell’avvolgimento.
Gli algoritmi automatici implementati attraverso il linguaggio di programmazione seguono i seguenti passi:
1) Viene simulata una bobina infinitesimale di superficie rettangolare. La superficie rettangolare è posta con il baricentro sull’origine degli assi cartesiani. All’inizio la superficie è suddivisa da due soli triangoli.
2) La bobina viene ruotata di un angolo assegnato per essere successivamente posizionata sullo statore.
3) La superficie viene traslata dall’origine degli assi sulla struttura statorica. In questo momento la mesh 2D viene sovrapposta alla mesh 3D sulla quale in precedenza è stata ricavata una soluzione di campo più accurata possibile.
4) Il flusso concatenato viene calcolato attraverso la (7-21).
5) La triangolazione 2D iniziale costituita da due soli triangoli viene rifinita. Il processo di refinement della mesh triangolare viene arrestato quando la variazione tra il valore del flusso concatenato in una iterazione non varia rispetto a quello calcolato nella iterazione precedente.
6) Per simulare il comportamento della bobina massiccia la spira viene spostata all’interno dell’avvolgimento di fase. L’avvolgimento viene simulato con un numero di bobine. Se il flusso concatenato è determinato su ognuna di queste spire la bobina massiccia sarà accuratamente simulata.
7) Dato che il flusso concatenato deve essere determinato su 180° elettrici la bobina massiccia non è mai completamente contenuta nel dominio 3D. Questa situazione è mostrata sulle proiezioni ortogonali della Figura 79. In questo caso la soluzione può essere ottenuta ruotando la superficie triangolare che non si trova nella mesh di 180° elettrici. La soluzione viene quindi ottenuta applicando le condizioni di antiperiodicità.
8) I valori del flusso concatenato determinati su 180° elettrici sono interpolati utilizzando il metodo cubic spline. La forma d’onda della fem indotta viene ottenuta derivando il polinomio di terzo grado.
Questo metodo risulta molto vantaggioso per la sua semplicità. Non è infatti necessario inserire l’avvolgimento di fase nella struttura 3D da triangolare. Il flusso concatenato può essere quindi facilmente determinato da un’unica soluzione MSP di campo per ogni posizione angolare.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 | Autori: Paolo Sordi Ordine degli ingegneri di Roma N° 22979 - Sezione A Leonardo Santini Ordine degli ingegneri di Roma N° 22757 - Sezione A RECURSIVE SUBROUTINE CALCOLO_FLUSSO_CONCATENATO_CON_SUPERFICIE_TRIANGOLARE (i_triangle,flusso_spira,i_stampa) USE IDENTIFIERS USE CONFIG_MESH_2D USE CONFIG_PARAMETRI IMPLICIT NONE INTEGER :: i_triangle, i_stampa DOUBLE PRECISION :: area DOUBLE PRECISION :: lato1,lato2,lato3 DOUBLE PRECISION :: semiperimetro DOUBLE PRECISION :: x1, y1, z1, x2, y2, z2, x3, y3, z3 DOUBLE PRECISION :: a, b, c, d DOUBLE PRECISION :: modulo_vett, flusso_spira DOUBLE PRECISION :: potenziale,diff_x,diff_y,diff_z DOUBLE PRECISION :: x_baricentro, Y_baricentro, Z_baricentro DOUBLE PRECISION :: pigreca,teta,raggio_modulo INTEGER :: in1, in2, in3 in1 = NT_2D (i_triangle,1) in2 = NT_2D (i_triangle,2) in3 = NT_2D (i_triangle,3) lato1 = DSQRT ((X_2D(in1)-X_2D(in2))**2.0 + (Y_2D(in1)-Y_2D(in2))**2.0 + (Z_2D(in1)-Z_2D(in2))**2.0) lato2 = DSQRT ((X_2D(in1)-X_2D(in3))**2.0 + (Y_2D(in1)-Y_2D(in3))**2.0 + (Z_2D(in1)-Z_2D(in3))**2.0) lato3 = DSQRT ((X_2D(in2)-X_2D(in3))**2.0 + (Y_2D(in2)-Y_2D(in3))**2.0 + (Z_2D(in2)-Z_2D(in3))**2.0) semiperimetro = (lato1 + lato2 + lato3) / 2.0 area = DSQRT (semiperimetro * (semiperimetro - lato1) * (semiperimetro - lato2) * (semiperimetro - lato3)) !WRITE (1000,*) "AREA", AREA x_baricentro = (X_2D(in1) + X_2D(in2) + X_2D(in3)) / 3.0 Y_baricentro = (Y_2D(in1) + Y_2D(in2) + Y_2D(in3)) / 3.0 Z_baricentro = (Z_2D(in1) + Z_2D(in2) + Z_2D(in3)) / 3.0 if (i_stampa.eq.1) CALL WDIALOGPUTREAL (IDF_REAL1 ,real (x_baricentro)) if (i_stampa.eq.1) CALL WDIALOGPUTREAL (IDF_REAL2 ,real (y_baricentro)) if (i_stampa.eq.1) CALL WDIALOGPUTREAL (IDF_REAL3 ,real (z_baricentro)) CALL CALCOLO_DEL_POTENZIALE_PER_IL_PUNTO_SPAZIALE (x_baricentro,Y_baricentro,Z_baricentro,potenziale,diff_x,diff_y,diff_z) CALL CALCOLO_DEL_PIANO_PER_TRE_PUNTI (X_2D(in1),Y_2D(in1),Z_2D(in1),X_2D(in2),Y_2D(in2),Z_2D(in2),X_2D(in3),Y_2D(in3),Z_2D(in3),A,B,C,D) modulo_vett = DSQRT (a**2 + b**2 + c**2) a = a / modulo_vett b = b / modulo_vett c = c / modulo_vett IF (potenziale.ne.0) THEN flusso_spira = a * diff_x + b * diff_y + c * diff_z if (i_stampa.eq.1) CALL WDIALOGPUTREAL (IDF_REAL4 ,real (diff_x)) if (i_stampa.eq.1) CALL WDIALOGPUTREAL (IDF_REAL5 ,real (diff_y)) if (i_stampa.eq.1) CALL WDIALOGPUTREAL (IDF_REAL6 ,real (diff_z)) flusso_spira = flusso_spira * area ELSE X_2D (NNOD_2D + 1) = X_2D (IN1) y_2D (NNOD_2D + 1) = Y_2D (IN1) Z_2D (NNOD_2D + 1) = Z_2D (IN1) y_2D (NNOD_2D + 2) = Y_2D (IN2) X_2D (NNOD_2D + 2) = X_2D (IN2) Z_2D (NNOD_2D + 2) = Z_2D (IN2) X_2D (NNOD_2D + 3) = X_2D (IN3) Y_2D (NNOD_2D + 3) = Y_2D (IN3) Z_2D (NNOD_2D + 3) = Z_2D (IN3) ! IL TRIANGOLO VIENE GIRATO PER APPLICARE LE CONDIZIONI DI ANTIPERIODICITA' IN1 = NNOD_2D + 2 IN2 = NNOD_2D + 1 IN3 = NNOD_2D + 3 NT_2D (NTRI_2D + 1,1) = IN1 NT_2D (NTRI_2D + 1,2) = IN2 NT_2D (NTRI_2D + 1,3) = IN3 CALL ROTAZIONE_DEL_TRIANGOLO_INDIETRO_DI_UN_POLO_DI_MACCHINA (x_2D(in1), Y_2D(in1), Z_2D(in1)) CALL ROTAZIONE_DEL_TRIANGOLO_INDIETRO_DI_UN_POLO_DI_MACCHINA (x_2D(in2), Y_2D(in2), Z_2D(in2)) CALL ROTAZIONE_DEL_TRIANGOLO_INDIETRO_DI_UN_POLO_DI_MACCHINA (x_2D(in3), Y_2D(in3), Z_2D(in3)) CALL CALCOLO_FLUSSO_CONCATENATO_CON_SUPERFICIE_TRIANGOLARE (NTRI_2D + 1, flusso_spira,i_stampa) RETURN END IF !WRITE (1000,*) '-------------------------------------------------------' !WRITE (1000,*) 'coordinate x,y,z baricentro',x_baricentro,y_baricentro,z_baricentro !WRITE (1000,*) 'a,b,c ', a,b,c !WRITE (1000,*) 'diff_x,diff_y,diff_z', diff_x,diff_y,diff_z !WRITE (1000,*) 'area ', area !WRITE (1000,*) 'flusso_spira', flusso_spira END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE ROTAZIONE_DEL_TRIANGOLO_INDIETRO_DI_UN_POLO_DI_MACCHINA(xp, yp, zp) USE WINTERACTER USE IDENTIFIERS USE CONFIG_AFPM USE CONFIG_MESH_2D USE CONFIG_PARAMETRI IMPLICIT NONE INTEGER :: i_triangle DOUBLE PRECISION :: area,gradi_meccanici180 DOUBLE PRECISION :: potenziale,diff_x,diff_y,diff_z DOUBLE PRECISION :: XP, YP, ZP DOUBLE PRECISION :: pigreca,teta,raggio_modulo CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRUNITS (REAL (ZMIN),REAL (YMIN),REAL (ZMAX),REAL (ymax)) CALL IGRCIRCLE (REAL (Zp), REAL (yp),0.5) pigreca = 4 * ATAN (1.) teta = ATAN (yp/zp) !WRITE (1000,*) 'teta', teta gradi_meccanici180 = 2 * pigreca / numero_poli teta = dabs (teta) - gradi_meccanici180 raggio_modulo = SQRT (zp ** 2.0 + yp ** 2.0) IF (yp.gt.0) THEN yp = - raggio_modulo * SIN (DABS(teta)) ELSE yp = + raggio_modulo * SIN (DABS(teta)) END IF zp = raggio_modulo * COS (teta) CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRUNITS (REAL (ZMIN),REAL (YMIN),REAL (ZMAX),REAL (ymax)) CALL IGRCIRCLE (REAL (Zp), REAL (yp), 0.5) END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE POSIZIONAMENTO_DELLA_BOBINA_SULLO_STATORE_MACCHINA () USE WINTERACTER USE IDENTIFIERS USE CONFIG_MESH USE CONFIG_PARAMETRI USE CONFIG_MESH_2D USE CONFIG_AFPM IMPLICIT NONE TYPE (win_message) :: MESSAGE DOUBLE PRECISION :: potenziale DOUBLE PRECISION :: potenz_x,potenz_y,potenz_z DOUBLE PRECISION :: vett_x, vett_y, vett_z DOUBLE PRECISION :: flusso_totale, flusso_spira DOUBLE PRECISION :: angolo_teta REAL :: xpoint,ypoint,zpoint REAL :: SCALa,v_min,V_max DOUBLE PRECISION :: altezza_bobina INTEGER :: i,itype,kk,kkk,i_conta,i_stampa CALL WDIALOGSELECT (IDD_DIALOG003) CALL WDIALOGSHOW (-1,-1,0,MODELESS) scala = 35.0 CALL WDIALOGPUTREAL (IDF_REAL8 ,REAL (scala)) CALL WDIALOGPUTINTEGER (idf_integer3 , NTETRA) CALL WDIALOGPUTINTEGER (idf_integer1 , NNOD) CALL WDIALOGPUTINTEGER (idf_integer2 , NLAT) CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRAREACLEAR () CALL CALCOLO_DEL_FATTORE_DI_SCALA_PER_LE_PROIEZIONI_ORTOGONALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) angolo_teta = 30 DO CALL WMESSAGE (ITYPE,MESSAGE) SELECT CASE (ITYPE) CASE (MOUSEBUTDOWN) SELECT CASE (MESSAGE%value1) CASE (1) CASE (3) END SELECT CASE (keydown) IF (MESSAGE%value1.EQ.27) THEN CALL WDIALOGUNLOAD() CALL IGRSELECT (Drawwin) CALL IGRAREACLEAR() RETURN END IF CASE (PUSHBUTTON) IF (MESSAGE%value1.eq.IDok) THEN CALL WDIALOGHIDE () CALL IGRSELECT (Drawwin) RETURN END IF IF (MESSAGE%value1.eq.IDabort2) THEN raggio_medio = ( raggio_interno + raggio_esterno ) / 2 altezza_bobina = raggio_esterno - raggio_interno asse_medio = 3 / 2 * spessore_statore + spessore_magneti + spessore_traferro CALL COSTRUZIONE_DELLA_BOBINA (asse_medio,spessore_statore,altezza_bobina,DBLE (0.0)) CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRAREACLEAR () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA END IF IF (MESSAGE%value1.eq.IDabort4) THEN CALL ROTAZIONE_RISPETTO_ASSE_X_DELLA_BOBINA (DBLE(angolo_teta)) CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRAREACLEAR () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA END IF IF (MESSAGE%value1.eq.IDabort3) THEN vett_x = 0 vett_y = raggio_medio * sin (3.1415926 * angolo_teta / 180) vett_z = raggio_medio * cos (3.1415926 * angolo_teta / 180) CALL SPOSTAMENTO_DELLA_BOBINA_PER_TRASLAZIONE (vett_x,vett_y,vett_z) CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRAREACLEAR () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA END IF IF (MESSAGE%value1.eq.IDabort5) THEN flusso_totale = 0.0 DO kk = 1 , NTRI_2D CALL CALCOLO_FLUSSO_CONCATENATO_CON_SUPERFICIE_TRIANGOLARE (kk, flusso_spira, i_stampa) flusso_totale = flusso_totale + flusso_spira END DO CALL WDIALOGPUTREAL (IDF_REAL7 ,REAL (flusso_totale)) END IF IF (MESSAGE%value1.eq.IDabort6) THEN CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRAREACLEAR () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA END IF IF (MESSAGE%value1.eq.IDabort7) THEN OPEN (1250, 'flusso concatenato.dat') i_conta = 0 DO i= 45 , -45, -5 angolo_teta = i CALL COSTRUZIONE_DELLA_BOBINA (asse_medio,spessore_statore,altezza_bobina,DBLE (0.0)) CALL ROTAZIONE_RISPETTO_ASSE_X_DELLA_BOBINA (DBLE(angolo_teta)) vett_x = 0 vett_y = raggio_medio * sin (3.1415926 * angolo_teta / 180) vett_z = raggio_medio * cos (3.1415926 * angolo_teta / 180) CALL SPOSTAMENTO_DELLA_BOBINA_PER_TRASLAZIONE (vett_x,vett_y,vett_z) CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE ! CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA flusso_totale = 0.0 DO kk = 1 , NTRI_2D CALL CALCOLO_FLUSSO_CONCATENATO_CON_SUPERFICIE_TRIANGOLARE (kk, flusso_spira, i_stampa) flusso_totale = flusso_totale + flusso_spira CALL WMESSAGEPEEK (ITYPE, MESSAGE) IF (ITYPE.eq.CLOSEREQUEST) STOP END DO ! Fino ad ora si è calcolato il flusso concatenato con la bobina di mezza macchina ! Per ottenere il flusso concatenato con l'intera bobina massiccia bisogna moltiplicare per due flusso_totale = flusso_totale * 2 ! WRITE (1250,*) flusso_totale CALL WDIALOGPUTREAL (IDF_REAL7 ,REAL (flusso_totale)) i_conta = i_conta + 1 vettore_flusso (i_conta) = flusso_totale CALL IGRSELECT (Drawfield,idf_picture4) CALL IGRAREACLEAR () v_min = MINVAL (vettore_flusso) v_max = MAXVAL (vettore_flusso) v_max = v_max + (MAXVAL (vettore_flusso) - MINVAL (vettore_flusso)) / 10 CALL IGRLINEWIDTH (2) CALL IGRUNITS (REAL (0.0),REAL (v_min),REAL (90.0),REAL (v_max)) ! CALL IGRMOVETO (0.0, 0.0) DO kkk = 0 , i_conta ! CALL IGRLINETO (real (kkk), vettore_flusso(kkk)) END DO CALL IGRLINEWIDTH (1) END DO CLOSE (1250) END IF IF (MESSAGE%value1.eq.IDabort8) THEN CALL CALCOLO_FLUSSO_SU_BOBINA_MASSICCIA (raggio_medio,asse_medio,spessore_statore,altezza_bobina, & spessore_bobina,numero_poli,1.0) END IF IF (MESSAGE%value1.eq.IDabort9) THEN CALL CALCOLO_DERIVATA_DEL_FLUSSO_CONCATENATO (1) END IF CASE (closerequest) STOP END SELECT END DO END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE CALCOLO_FLUSSO_SU_BOBINA_MASSICCIA (raggio_medio,asse_medio,spessore_statore,altezza_bobina, & spessore_bobina,num_poli_macchina, i_stampa) USE WINTERACTER USE IDENTIFIERS USE CONFIG_MESH_2D USE CONFIG_AFPM, ONLY : vettore_flusso IMPLICIT NONE TYPE (win_message) :: MESSAGE DOUBLE PRECISION :: raggio_medio, asse_medio, spessore_statore, altezza_bobina DOUBLE PRECISION :: vett_x, vett_y, vett_z DOUBLE PRECISION :: angolo_teta DOUBLE PRECISION :: flusso_totale, flusso_spira DOUBLE PRECISION :: spessore_bobina,spessore_spira INTEGER :: i,itype,kk,k,kkk,numero_spire INTEGER :: num_div_rad,num_div_ass,num_poli_macchina INTEGER :: i_conta, i_stampa REAL :: xpoint,ypoint,zpoint REAL :: scala,v_min,V_max OPEN (1150, 'flusso concatenato bobina massiccia.dat') num_div_rad = 2 num_div_ass = 1 i_conta = 0 DO i = 90 , -90, -2 !DO i = 0 , -90, -2 flusso_totale = 0.0 angolo_teta = real (i) / (real (num_poli_macchina) / 2.) ! WRITE (1000,*) 'angolo_teta',angolo_teta CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRAREACLEAR () CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRAREACLEAR () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DEI_MATERIALI () CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) numero_spire = 0 DO k = -num_div_rad , num_div_rad DO kkk = 0 , num_div_ass spessore_spira = spessore_bobina * kkk / real (num_div_ass) ! WRITE (1000,*) 'spessore_spira',spessore_spira ! WRITE (1000,*) 'entrata' CALL COSTRUZIONE_DELLA_BOBINA (asse_medio,spessore_statore,altezza_bobina,spessore_spira) CALL ROTAZIONE_RISPETTO_ASSE_X_DELLA_BOBINA (DBLE(angolo_teta)) vett_x = 0 vett_y = raggio_medio * sin (3.1415926 * angolo_teta / 180.) vett_z = raggio_medio * cos (3.1415926 * angolo_teta / 180.) CALL SPOSTAMENTO_DELLA_BOBINA_PER_TRASLAZIONE (vett_x,vett_y,vett_z) CALL SPOSTAMENTO_DELLA_BOBINA_PER_SIMULAZIONE_MASSICCIA (k, num_div_rad,raggio_medio, altezza_bobina, & spessore_bobina, num_poli_macchina) ! WRITE (1000,*) 'uscita' CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE ! CALL RIFINISCI_LA_MESH_BIDIMENSIONALE_CON_CRITERIO_FRATTALE CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_X_CARCIOFO (0) CALL DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA numero_spire = numero_spire + 1 DO kk = 1 , NTRI_2D CALL CALCOLO_FLUSSO_CONCATENATO_CON_SUPERFICIE_TRIANGOLARE (kk, flusso_spira, i_stampa) flusso_totale = flusso_totale + flusso_spira CALL WMESSAGEPEEK (ITYPE, MESSAGE) IF (MESSAGE%value1.eq.IDok) THEN RETURN END IF IF (ITYPE.eq.CLOSEREQUEST) STOP END DO CALL WDIALOGPUTREAL (IDF_REAL7 ,REAL (flusso_totale)) END DO END DO ! flusso concatenato medio con la bobina massicia flusso_totale = flusso_totale / real (numero_spire) ! Fino ad ora si è calcolato il flusso concatenato con la bobina di mezza macchina ! Per ottenere il flusso concatenato con l'intera bobina massiccia bisogna moltiplicare per due flusso_totale = flusso_totale * 2 i_conta = i_conta + 1 vettore_flusso (i_conta) = flusso_totale CALL IGRSELECT (Drawfield,idf_picture4) CALL IGRAREACLEAR () CALL WDIALOGCOLOUR (idf_picture4,WIN_RGB(128,128,0),WIN_RGB(128,128,0)) CALL WINDOWFONTCOLOUR (5,10) v_min = MINVAL (vettore_flusso) v_max = MAXVAL (vettore_flusso) v_max = v_max + (MAXVAL (vettore_flusso) - MINVAL (vettore_flusso)) / 10. CALL IGRLINEWIDTH (2) CALL IGRUNITS (REAL (0.0),REAL (v_min),REAL (90.0),REAL (v_max)) CALL IGRMOVETO (0.0, 0.0) DO kkk = 1 , i_conta CALL IGRLINETO (real (kkk), real (vettore_flusso(kkk))) END DO CALL IGRLINEWIDTH (1) END DO CLOSE (1150) END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE SPOSTAMENTO_DELLA_BOBINA_PER_SIMULAZIONE_MASSICCIA (k, num_div_rad,raggio_medio, altezza_bobina, & spessore_bobina, num_poli_macchina) USE CONFIG_MESH_2D IMPLICIT NONE DOUBLE PRECISION :: raggio_medio, asse_medio, spessore_statore, altezza_bobina DOUBLE PRECISION :: spessore_bobina,spessore_rame DOUBLE PRECISION :: pigreca,modulo_vett,raggio_minimo_rame,modulo_traslazione DOUBLE PRECISION :: a,b,c,d DOUBLE PRECISION :: teta, coseno INTEGER :: k, i, kk, num_div_rad INTEGER :: in1, in2, in3 INTEGER :: num_poli_macchina pigreca = 4 * ATAN (1.) in1 = NT_2D (1,1) in2 = NT_2D (1,2) in3 = NT_2D (1,3) CALL CALCOLO_DEL_PIANO_PER_TRE_PUNTI (X_2D(in1),Y_2D(in1),Z_2D(in1),X_2D(in2),Y_2D(in2),Z_2D(in2),X_2D(in3),Y_2D(in3),Z_2D(in3),A,B,C,D) modulo_vett = DSQRT (a**2 + b**2 + c**2) a = a / modulo_vett b = b / modulo_vett c = c / modulo_vett raggio_minimo_rame = raggio_medio - (altezza_bobina / 2.0) - spessore_bobina !WRITE (1000,*) 'raggio_minimo_rame',raggio_minimo_rame spessore_rame = 2 * pigreca * raggio_minimo_rame/ (num_poli_macchina * 3 * 2) modulo_traslazione = spessore_rame * k / num_div_rad a = a * modulo_traslazione b = b * modulo_traslazione c = c * modulo_traslazione DO KK = 1, NNOD_2D X_2D (kk) = X_2D (kk) + a Y_2D (kk) = Y_2D (kk) + b Z_2D (kk) = Z_2D (kk) + c END DO teta = ASIN (modulo_traslazione / raggio_medio) coseno = raggio_medio * COS (teta) DO KK = 1, NNOD_2D Z_2D (kk) = Z_2D (kk) - (raggio_medio - coseno) END DO END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE DISEGNA_LE_PROIEZIONI_ORTOGONALI_DELLA_BOBINA USE winteracter USE IDENTIFIERS USE CONFIG_MESH_2D USE CONFIG_PARAMETRI CALL IGRLINEWIDTH (2) CALL IGRCOLOURN (223) CALL IGRSELECT (Drawfield,idf_picture1) CALL IGRUNITS (REAL (XMIN),REAL (YMIN),REAL (XMAX),REAL (ymax)) DO KK = 1, NTRI_2D CALL IGRMOVETO (REAL (X_2D(NT_2D (KK,1))), REAL (Y_2D(NT_2D (KK,1)))) CALL IGRLINETO (REAL (X_2D(NT_2D (KK,2))), REAL (Y_2D(NT_2D (KK,2)))) CALL IGRLINETO (REAL (X_2D(NT_2D (KK,3))), REAL (Y_2D(NT_2D (KK,3)))) CALL IGRLINETO (REAL (X_2D(NT_2D (KK,1))), REAL (Y_2D(NT_2D (KK,1)))) END DO CALL IGRSELECT (Drawfield,idf_picture3) CALL IGRUNITS (REAL (XMIN),REAL (-ZMAX),REAL (XMAX),REAL (-ZMIN)) DO KK = 1, NTRI_2D CALL IGRMOVETO (REAL (X_2D(NT_2D (KK,1))), REAL (-z_2D(NT_2D (KK,1)))) CALL IGRLINETO (REAL (X_2D(NT_2D (KK,2))), REAL (-Z_2D(NT_2D (KK,2)))) CALL IGRLINETO (REAL (X_2D(NT_2D (KK,3))), REAL (-Z_2D(NT_2D (KK,3)))) CALL IGRLINETO (REAL (X_2D(NT_2D (KK,1))), REAL (-Z_2D(NT_2D (KK,1)))) END DO CALL IGRSELECT (Drawfield,idf_picture2) CALL IGRUNITS (REAL (ZMIN),REAL (YMIN),REAL (ZMAX),REAL (ymax)) DO KK = 1, NTRI_2D CALL IGRMOVETO (REAL (z_2D(NT_2D (KK,1))), REAL (Y_2D(NT_2D (KK,1)))) CALL IGRLINETO (REAL (Z_2D(NT_2D (KK,2))), REAL (Y_2D(NT_2D (KK,2)))) CALL IGRLINETO (REAL (Z_2D(NT_2D (KK,3))), REAL (Y_2D(NT_2D (KK,3)))) CALL IGRLINETO (REAL (Z_2D(NT_2D (KK,1))), REAL (Y_2D(NT_2D (KK,1)))) END DO CALL IGRLINEWIDTH (1) END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE COSTRUZIONE_DELLA_BOBINA (asse_medio,spessore_statore,altezza_bobina, spessore_spira) USE CONFIG_MESH_2D USE WINTERACTER IMPLICIT NONE INTEGER :: in1,in2,in3 INTEGER :: i DOUBLE PRECISION :: raggio_medio, asse_medio, spessore_statore, altezza_bobina, spessore_spira DOUBLE PRECISION :: a1,b1,c1,d1,a,b,c,d X_2D (1) = asse_medio + spessore_statore Y_2D (1) = 0 Z_2D (1) = - altezza_bobina / 2.0 - spessore_spira X_2D (2) = asse_medio - spessore_spira Y_2D (2) = 0 Z_2D (2) = - altezza_bobina / 2.0 - spessore_spira X_2D (3) = asse_medio + spessore_statore Y_2D (3) = 0 Z_2D (3) = altezza_bobina / 2.0 + spessore_spira X_2D (4) = asse_medio - spessore_spira Y_2D (4) = 0 Z_2D (4) = altezza_bobina / 2.0 + spessore_spira NT_2D (1,1) = 1 NT_2D (1,2) = 2 NT_2D (1,3) = 4 NT_2D (2,1) = 3 NT_2D (2,2) = 1 NT_2D (2,3) = 4 NNOD_2D = 4 NTRI_2D = 2 in1 = NT_2D (1,1) in2 = NT_2D (1,2) in3 = NT_2D (1,3) CALL CALCOLO_DEL_PIANO_PER_TRE_PUNTI (X_2D(in1),Y_2D(in1),Z_2D(in1),X_2D(in2),Y_2D(in2),Z_2D(in2),X_2D(in3),Y_2D(in3),Z_2D(in3),A1,B1,C1,D1) !WRITE (1000,*) 'a1,b1,c1,d1',a1,b1,c1,d1 DO i = 1 , NTRI_2D in1 = NT_2D (i,1) in2 = NT_2D (i,2) in3 = NT_2D (i,3) CALL CALCOLO_DEL_PIANO_PER_TRE_PUNTI (X_2D(in1),Y_2D(in1),Z_2D(in1),X_2D(in2),Y_2D(in2),Z_2D(in2),X_2D(in3),Y_2D(in3),Z_2D(in3),A,B,C,D) ! WRITE (1000,*) 'a,b,c,d',a,b,c,d IF (a.ne.a1.or.b.ne.b1.or.c.ne.c1) THEN CALL WMESSAGEBOX (0,0,1,'non tutti i triangoli sono orientati allo stesso modo','') STOP END IF END DO END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE ROTAZIONE_RISPETTO_ASSE_X_DELLA_BOBINA (angolo_teta) USE CONFIG_MESH_2D IMPLICIT NONE DOUBLE PRECISION :: vett_x, vett_y, vett_z INTEGER kk DOUBLE PRECISION :: angolo_teta , angolo_rad angolo_rad = 3.1415926 * angolo_teta / 180 !WRITE (1000,*) 'angolo_teta',angolo_teta !WRITE (1000,*) 'angolo_rad',angolo_rad DO KK = 1, NNOD_2D Y_2D (kk) = Z_2D (kk) * SIN (angolo_rad) Z_2D (kk) = Z_2D (kk) * COS (angolo_rad) END DO END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE SPOSTAMENTO_DELLA_BOBINA_PER_TRASLAZIONE (vett_x,vett_y,vett_z) USE CONFIG_MESH_2D IMPLICIT NONE DOUBLE PRECISION :: vett_x, vett_y, vett_z INTEGER kk DO KK = 1, NNOD_2D X_2D (kk) = X_2D (kk) + vett_x Y_2D (kk) = Y_2D (kk) + vett_y Z_2D (kk) = Z_2D (kk) + vett_z END DO END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE CALCOLO_DEL_POTENZIALE_SUL_NODO (itetra, XP, YP, ZP,potenziale,diff_x,diff_y,diff_z) USE CONFIG_MESH USE CONFIG_FEM USE CONFIG_AFPM USE WINTERACTER IMPLICIT NONE TYPE (win_message) :: MESSAGE INTEGER itype DOUBLE PRECISION, DIMENSION (4,4) :: matrix_ABCD INTEGER itetra DOUBLE PRECISION :: potenziale DOUBLE PRECISION :: XP,YP,ZP DOUBLE PRECISION :: a,b,c,d DOUBLE PRECISION :: diff_x,diff_y,diff_z diff_x = 0 diff_y = 0 diff_z = 0 CALL CALCOLA_COEFFICIENTI_A_B_C_D (itetra, matrix_ABCD) ! calcolo i coefficienti A, B, C, D della funzione ! U(x,y,z) = A + B x + C y + D z a = matrix_ABCD(1,1) * FUNZIONE_SCALARE (NT(itetra,1)) + & matrix_ABCD(1,2) * FUNZIONE_SCALARE (NT(itetra,2)) + & matrix_ABCD(1,3) * FUNZIONE_SCALARE (NT(itetra,3)) + & matrix_ABCD(1,4) * FUNZIONE_SCALARE (NT(itetra,4)) b = matrix_ABCD(2,1) * FUNZIONE_SCALARE (NT(itetra,1)) + & matrix_ABCD(2,2) * FUNZIONE_SCALARE (NT(itetra,2)) + & matrix_ABCD(2,3) * FUNZIONE_SCALARE (NT(itetra,3)) + & matrix_ABCD(2,4) * FUNZIONE_SCALARE (NT(itetra,4)) c = matrix_ABCD(3,1) * FUNZIONE_SCALARE (NT(itetra,1)) + & matrix_ABCD(3,2) * FUNZIONE_SCALARE (NT(itetra,2)) + & matrix_ABCD(3,3) * FUNZIONE_SCALARE (NT(itetra,3)) + & matrix_ABCD(3,4) * FUNZIONE_SCALARE (NT(itetra,4)) d = matrix_ABCD(4,1) * FUNZIONE_SCALARE (NT(itetra,1)) + & matrix_ABCD(4,2) * FUNZIONE_SCALARE (NT(itetra,2)) + & matrix_ABCD(4,3) * FUNZIONE_SCALARE (NT(itetra,3)) + & matrix_ABCD(4,4) * FUNZIONE_SCALARE (NT(itetra,4)) potenziale = a + b * XP + c * YP + d * ZP diff_x = b diff_y = c diff_z = d IF (MATERIALE_TETRAEDRO (itetra).EQ.2) THEN diff_x = diff_x * PERMEABILITA_RELATIVA_FERRO diff_y = diff_y * PERMEABILITA_RELATIVA_FERRO diff_z = diff_z * PERMEABILITA_RELATIVA_FERRO END IF END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE SVILUPPO360SFASATODIUNO(curva360,curva_180) IMPLICIT NONE DOUBLE PRECISION :: curva_180(0:180) DOUBLE PRECISION :: curva360(361) INTEGER :: i curva360(1) = curva_180(90) DO i = 1 , 90 curva360(i+1) = curva_180(90+i) curva360(90+i+1) = - curva_180(i) curva360(180+i+1) = - curva_180(90+i) curva360(270+i+1) = curva_180(i) END DO RETURN END |
APPLICAZIONE SU TRE CONFIGURAZIONI DI MACCHINA
Il calcolo delle fem a vuoto viene provato su una macchina a flusso assiale a due coppie di poli. Nelle Figure 7-11, 12, 13 sono riportati i profili di tre diversi tipi di magneti permanenti montati sui dischi rotorici.
Di queste tre configurazione bisogna determinare il flusso concatenato e la fem indotta a vuoto per velocità angolare unitaria. Dato che i magneti permanenti sono i componenti più costosi presenti in una macchina a flusso assiale è possibile anche richiedere dei profili di qualsivoglia forma e profilo.
Figura – Vista della struttura con magneti permanenti con profilo trapezoidale (passo del magnete τm=60°). Nel grafico sono riportati il flusso concatenato e la fem indotta su 360° elettrici.
Figura – Vista della struttura con magneti permanenti con profilo trapezoidale (passo del magnete τm=54°). Nel grafico sono riportati il flusso concatenato e la fem indotta su 360° elettrici.
Figura – Vista della struttura con magneti permanenti con profilo rettangolare. Nel grafico sono riportati il flusso concatenato e la fem indotta su 360° elettrici.
I magneti permanenti possono essere incassati sul disco rotorico senza il fissaggio attraverso fori e viti di bloccaggio.
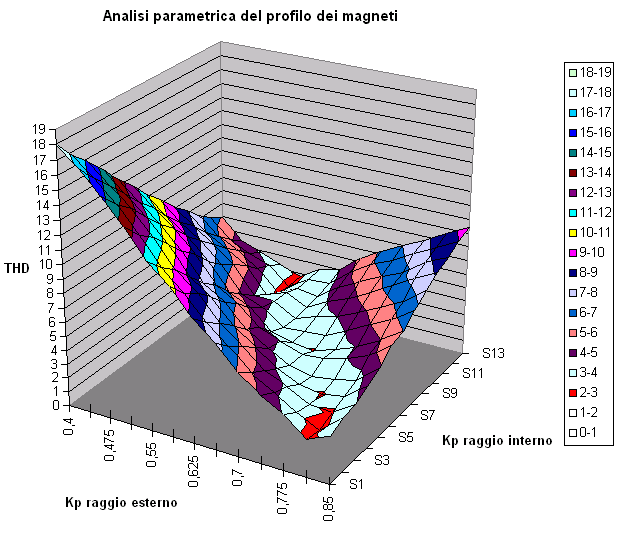
In Figura è riportato lo studio parametrico per l’analisi del fattore di distorsione armonica della FEM indotta. I valori riportati provengono dallo studio di 12×12 = 144 macchine la cui struttura è definita dai seguenti parametri: numero di poli = 16; Raggio esterno del disco rotorico = 120 mm; Raggio interno = 90 mm. Sui due assi vengono variati due parametri: Le quote parti di passo occupate dal magnete sul raggio esterno e sul raggio interno. In pratica sulla stessa struttura di macchina sono montati 144 diversi magneti permanenti. Dal grafico si evince che un numero elevato di configurazioni permette di raggiungere valori del THD minori del 4%. Solo un numero limitato di macchine riescono ad abbassare la distorsione armonica al di sotto del 3%.
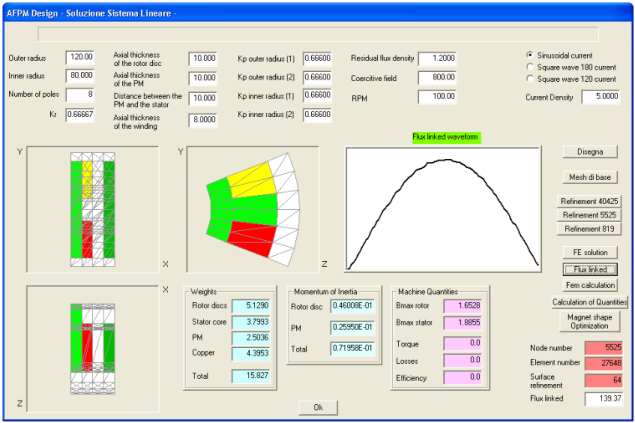
Se una soluzione numerica diventa accettabile la configurazione di macchina da realizzare può essere simile a quella calcolata. La soluzione del flusso concatenato e della fem sono dedotte da una soluzione agli elementi finiti contenente 40894 nodi.
La Figura riporta la finestra di dialogo principale per il progetto della macchina. I campi posti sulla parte alta della finestra sono gli input del dimensionamento. Nella parte bassa della finestra vengono riportati i risultati del calcolo numerico.
Il vantaggio operativo di una soluzione scalare è che il peso computazione nella risoluzione del sistema di equazioni non viene triplicato. Con 40894 nodi la soluzione del sistema di equazioni lineari di dimensioni (n x n) prevede un tempo di risposta di un processore a 1300 MHz di circa 13 minuti (solutore del sistema lineare: metodo del gradiente). Per avere la stessa precisione numerica con il potenziale vettore il peso computazionale viene triplicato.
La Figura 7-16 riporta il passaggio riguardante lo studio in serie di Fourier della forma d’onda del flusso concatenato. Attraverso le componenti armoniche di viene determinato il valore delle componenti armoniche della fem indotta. La pulsazione angolare viene determinata una volta inserita la velocità angolare della macchina in un campo mostrato nella Figura 7-15.